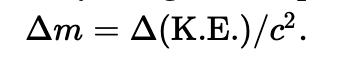翻译自费曼的物理学讲义,大致翻译完,余下“质能等效”一节,以及一些文字矫正的工作。
符号约定
SQ: 取一个数的平方SQRT: 取一个数的平方根×: 乘法符号m * n: m 乘以 nm / n: m 除以 n
目录
- 相对性原则
- 洛伦兹变换
- 迈克尔森-莫雷实验
- 时间变换
- 空间变换
- 同时性
- 四维向量
- 动力学相对性
- 质能等效(TODO)
相对性原则
过去 200 余年里,牛顿提出的运动方程被认为是对自然的正确描述,而这个自然定律存在的问题首次被发现的时候,解决的方法也一同被提出。此二者均由爱因斯坦于 1905 年提出。
牛顿第二定律,被我们描述为以下形式:
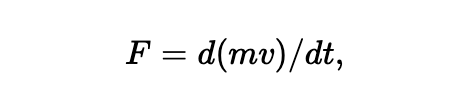
它假设了 m 是一个常量,但是我们现在知道,这不正确,物体的质量是随着速度的增加而增加的。在爱因斯坦修正后的方程里 m 的值以如下形式给出:
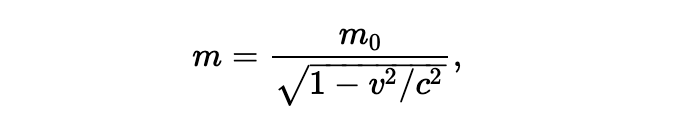
这里,“静态质量” m0 被定义为物体在静止时候的质量;c 是光的速度,也就是 3×105 km/s,近似为 186,000 mi/sec。
对于那些仅仅想解决问题的人来说,上面这些知识就是相对论的全部了——它不过通过引入一个质量修正因子来纠正牛顿定律。从上面的公式可以看出,通常情况下,质量增加得非常微小。即使以一颗人造卫星的速度,它每秒围绕地球行进 5 迈,因而 v/c 的值就是 5/186000,把这个值放到公式里,得到的质量修正量只有二十到三十亿分之一,这个变化几乎不可能被观测到。实际上,对许多高速粒子的观测已经充分证实了这个公式的正确性,这些粒子的运动速度往往接近光速。然而,效应如此微弱,以至于理论的提出先于实验观测。经验上来说,如果速度足够高,效应会非常显著,但是我们也无法用正常方式观察到它。因此,如何使用物理实验和推论来对这个微妙的修正加以检测,从而让它被广为接受,是一件非常有意思的事。许多人都在尝试解决这个问题,而最终成功的人是爱因斯坦。
爱因斯坦的相对论有两个,我们这章只是关注狭义相对论,它于 1905 年被发现。在 1915 年,爱因斯坦发表了一个补充理论,称为广义相对论。后者产生的目的是为解决重力问题而对狭义理论的一个推广,我们不在此讨论它。
相对性原则最开始是由牛顿提出的,它是牛顿运动定律下的一个必然结论。
给定空间中的物体的运动在它们自身来说都是一样的,不管这个空间是静止还是匀速地沿着直线运动。
这意味着,比如说,一个宇宙飞船以匀速运动,那么在这个飞船内的全部实验结论、现象,和这个飞船在静止的情况下表现一致,当然假设主体(人)不向窗外看。这就是相对性原则的意思。这是个非常简单明了的观点,唯一的问题是静止和运动系统中的物理实验是否表现一致。我们先来看看牛顿的定律是否在动系下表现一致。
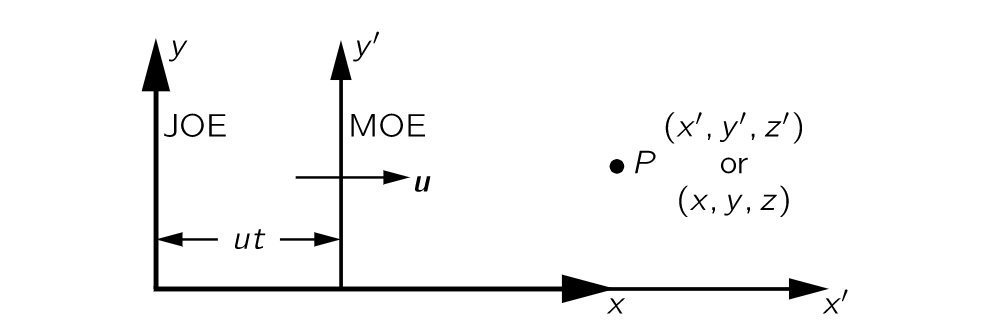
假设 Moe 沿着 x 方向匀速移动,速度为 u,并且他标记了某个点 P 的位置,如上图。他表示这个点的在 x 方向上的距离是 x’。Joe 是静止的,他也测量了 P 的位置,在他的系统下 P 在 x 方向上的距离是 x。从上图可以清楚的知道 x 和 x’ 的关系。时间过去了 t 个单位,Moe 所在系统的原点移动了一个距离 ut,这里假设两个系统原本是重合的。
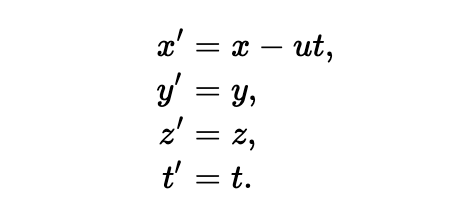
如果我们将这个转换用到牛顿的力学方程中,就会发现转换后的形式跟转换之前是一样的。也就是说,牛顿定律的形式在静系和在动系中保持不变。也因此,我们无法通过物理实验来检测到系统的静与动。
相对性原则已经在动力学中被接受了很长时间。许多人,尤其是 Huygens(惠更斯),曾使用它来研究桌球碰撞的规律,第 10 章我们会用相同的方法来探究动量守恒。19 世纪人们对电磁和光现象的研究投入颇多,也是在此时,人们对相对性原则的兴趣重新被激发。对有关电磁现象的大量细致的研究以 Maxwell 的电磁场方程的问世而告终,该方程对电、磁、光进行了统一描述。然而,Maxwell 的方程好像违反了相对性原则!就是说,如果我们对该方程应用以上转换,前后的形式是不一致的。因此,在一个运动的飞船里,光电现象会和在一个静止的飞船中表现得不同。人们因而可以通过一些光电实验计算出飞船的绝对速度。Maxwell 的方程推论之一就是,由某处场的扰动而产生的电磁波会以一致的速度,光速 c,也就是 186000 mi/sec,向各个方向传播。另一个推论是如果扰动源是运动的,由其产生的光还是会以速度 c 向外传播。这和声音的传播是类似的,声波的速度与声源的运动无关。
光的这种与源的运动的无关性导致了一个有趣的问题:
假设我们以速度 u 开着一辆车,一束光以速度 c 从后边追上来,对上述方程求导得到:
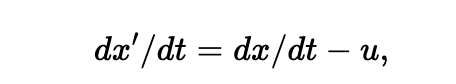
显然,根据伽利略转换,我们在车里测量到这一束光的速度不会是 c,而应该是 c - u。例如,如果汽车以 100000 mi/sec 的速度运行,这束光的速度是 186000 mi/sec,那么光通过汽车的速度就是 86000 mi/sec。无论什么情况,只要我们测量一下光通过汽车的时速度就能知道汽车的速度,这里我们假设伽利略转换对于光是正确的。基于这个想法,大量的实验企图测量出地球的速度,但是均以失败告终 —— 所有的实验测得的速度都是0。我们将具体看一下其中一个实验,以准确的了解当时做了什么以及问题是什么;一定哪里有问题,当然,是物理方程出了问题。那可能是什么呢?
洛伦兹变换
当上述物理方程的问题呈现于世的时候,首先为人们所想到的是 Maxwell 的电动方程必定隐藏了某种错误,当时离它问世不过 20 年。人们起初非常确信这个方程存在问题,因此试图找出某种修正方法以使其在伽利略变换下形式保持不变。一番尝试之后,一个新项的引入导致方程预测出一种根本不能被验证到的电现象,因此这种思路不得不被放弃。人们逐渐意识到 Maxwell 的电动方程是正确的,问题在别的地方。
与此同时,洛伦兹(H. A. Lorentz)发现了一个重要而新奇的事情,当他对 Maxwell 方程应用以下替换之后:
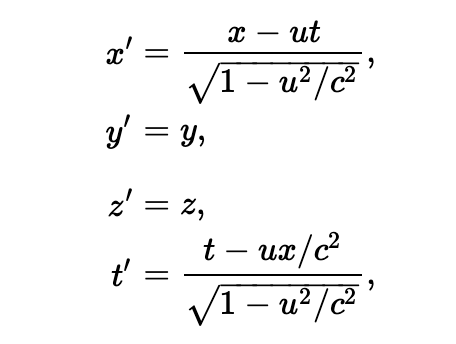
Maxwell 的方程形式上保持了不变。上述变换就是著名的洛伦兹变换。爱因斯坦追随 Poincaré 最初的意见,提出全部的物理定律必须在洛伦兹变换下保持形式的不变。换句话,我们不应该修改电动学定律,而应该修改力学定律。我们如何修改牛顿的力学定律来使之对洛伦兹变换下形式不变呢?如果设立了这个目标,我们就需要修改牛顿方程以使之满足我们上面提到的那些条件。结论是,我们只需要修改牛顿力学方程中的质量项。这样修改之后,牛顿定律就和电动力学定律相和谐。这时,我们通过一番变换之后,再对 Moe 和 Joe 的测量结果进行比较,就无法知道究竟是谁在运动了,因为在两个系统中物理学方程的形式是一样的。
探讨一下新的变换的意义是有趣的,因为伽利略变换看起来是自明的,而洛伦兹变换是晦涩的。我们希望知道是否在逻辑上和在实验上来说,是洛伦兹变换而非伽利略变换,是正确的。为了一探究竟,仅仅研究力学定律是不够的,正如爱因斯坦说的,我们必须同时分析我们的时空观念,才能理解这个新的变换。我们必须在一定程度上讨论这些观点以及这些观点对力学的影响,可以提前告知各位这些工作是值得的,因为结论跟实验是相符的。
迈克尔森-莫雷实验

如上所述,人们试图得到地球通过以太时的绝对速度,以太是一种假想的媒质,它充满了整个宇宙空间。最著名的实验由 Michelson 和 Morley 在 1887 年完成。18 年之后,实验的否定结论才最终得到解释,这源自爱因斯坦。
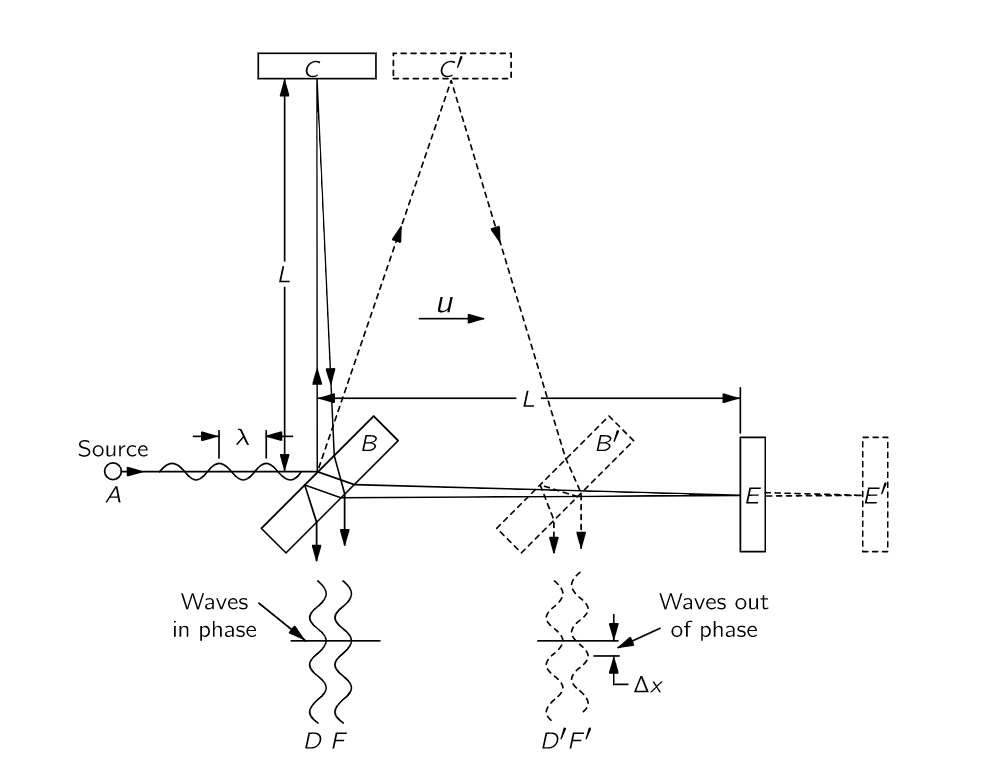
上图示意了 Michelson-Morley 当时实验所用到的设备。它由一个光源 A、一个半银质的玻璃盘 B(下边以 B 代指)、两面镜子 C(下边以 C 代指) 和 E(下边以 E 代指),它们都被固定在一个坚硬的基座上。两面镜子与 B 的距离都是 L。B 将光束一分为二,两束光彼此垂直地射向镜子 C 和 E,然后被镜子反射回 B。二者在 B 处汇聚,形成干涉光 D 和 F。如果光束经过 BE 的时间和经过 BC 的时间相等,那么 D 和 F 将同相增强。但是,如果这两个时间有轻微的不同,那么 D 和 F 就会不同相,从而出现干涉现象。如果设备相对以太是静止的,那么这两个时间应该相等;但是如果它以速度 u 自左向右运动,时间将不相等。先让我们看看这是为什么。
首先,让我们计算一下光从 B 到 E 并回到 B 所需的时间。设从 B 到 E,光跑完需要的时间为 t1,返回到 B 所需的时间为 t2。现在,光在 B 处,正射向镜子,设备运动了一段距离 ut1,因此光必需经过的距离是 L + ut1,以光速 c。我们可以将这个距离写为 ct1,因此我们得到:
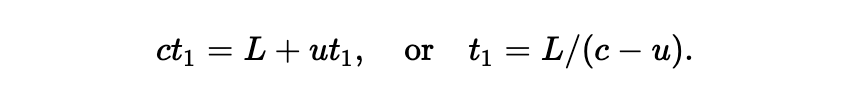
(从光相对设备的速度是 c - u 这点看来,此结果是显然的,如此,所需的时间就是距离 L 除以 (c - u) 以类似的方式,我们可以计算出 t2。这期间 B 前进了一段距离 ut2,因此光折返的距离就是 L - ut2。于是,我们得到:
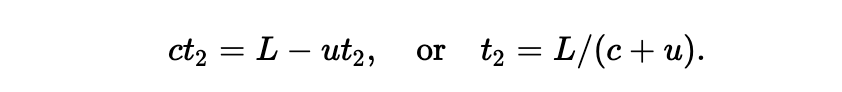
继而,总的时间为:
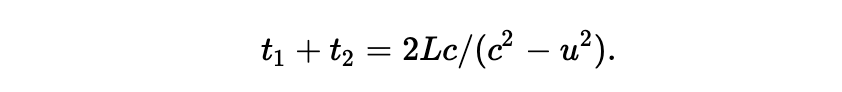
为了后续对时间进行比较之便,我们将其写为:
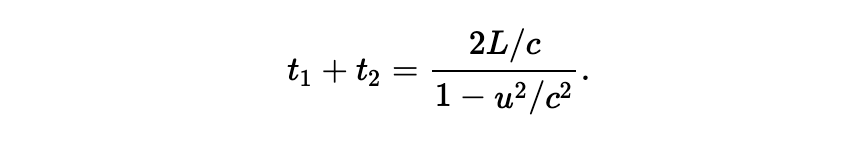
我们的第二个计算是 t3,它是光从 B 到 C 所需的时间。经过时间 t3,C 移动到新的位置 C’,距离为 ut3;与此同时,光沿着三角形的弦运行了距离 ct3,标记为 BC’。 借助右侧的三角形,我们得到:
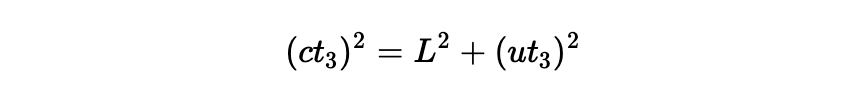
或:
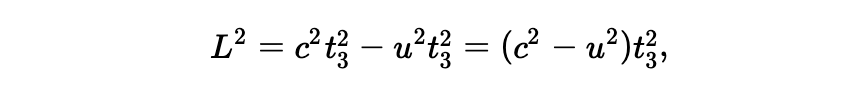
由此,我们有:
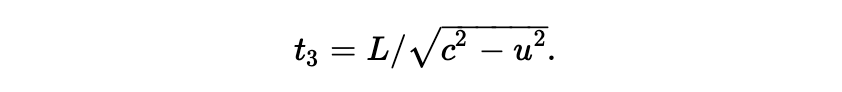
从对称性可以看出,由 C’ 折返的距离与此相等;因此折返的时间也是相等的,那么总的时间就是 2t3。稍微经过编排,我们可以写出:
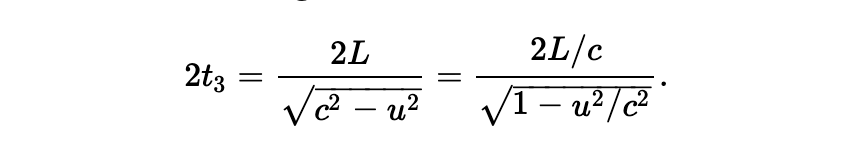
我们现在就可以比较两束光运行所耗的时间。在表达式 Eq#4 和 Eq#5 中,分子是一样的,它表示的是设备静止时光需要的时间。看看分母,项 u2/c2 会非常小,除非 u 与 c 有可比较性。分母表示的是设备的移动对时间的修正。注意看,这个修正因子是不一样的,光行至 C 并返回所需的时间稍微小于 E,即便这两面镜子与 B 的距离相等,我们要做的就是精确的测量出这个差异。
这里有一个小的技术问题,我们能假设两个距离是 100% 相等的么?实际上,我们当然不能确保它们完全相等。基于此,我们简单的将设备转动 90 度,使得 BC 在地球轨道的方向上,而 BE 与之垂直。任何长度上的差异就变得无关紧要了,接下来我们需要寻找就是由转动设备引起的干涉条纹的移动。
实验中,Michelson 和 Morley 将 BE 调整到接近地球的轨道行进的方向(在一个具体的时间点)。地球的轨道速度为 18 mi/sec,那么以太就会以差不多的速度后退(具体的时间上)。设备的灵敏度足够察觉到这个移动效应,然而时间差并未被测量到,地球相对以太的速度也无法得到。实验的结果是一场空。
Michelson 和 Morley 的实验结果是让人困扰、疑惑的。为打破僵局,首个富有成效的解决思路是洛伦兹想到的。他建议有质量的物体在运动的时候会发生长度上的收缩,并且收缩只发生在运动的方向上,并且如果物体静止时的长度是 L0,那么它在长度方向上以速度 u0 运行的时候,有一个新的长度,我们称之为 L||,按照如下公式给出:
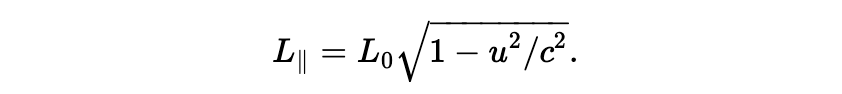
当这个修正应用到 Michelson-Morley 的干涉仪上时,B 到 C 的距离不变,但是 B 到 E 的距离缩短到:
L * SQRT(1 - (u/c)2)
因此 Eq#5 不变,但是 Eq#6 中的 L 必需按照上边的变换加以修改。操作一番,我们就得到:
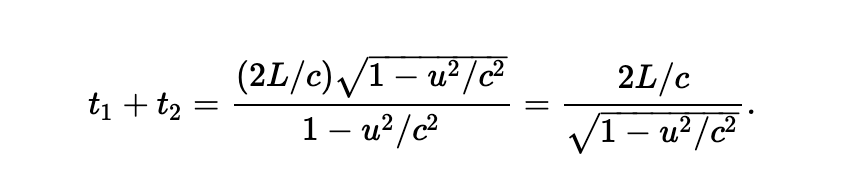
将其与 Eq#5 相比,我们看到 t1+t2=2t3。因此如果设备按上述方式收缩,我们就能理解为什么 Michelson- Morley 的实验未能给出任何差异。即便我们将洛伦兹的收缩假说考虑进来,解释了实验的否定结果,我们仍然对此表示反对,因为这是为了回避困难而发明出来的东西,过于人为。然而,许多其它企图检测以太风的实验,都会存在类似的困难,事情最终看起来似乎是大自然的一个阴谋,它引进一个新的现象来遮盖其它相关现象,以此它认为可以阻挠人类测量到地球的绝对速度。
最终我们意识到,就如 Poincaré 指出的,全部的阴谋本就是自然的定律。Poincaré 随后提议存在一种自然定律,那就是:无法采取任何实验的方式发现以太风。这也就是说,我们无论如何都无法测量到绝对速度。
时间变换
在检验尺度收缩理论是否与其它实验结果相符合的过程中,终于发现全部的结论都符合,只要我们再对时间做一个类似形式(Eq#3)的变换。因为从 B 出发到达 C 再返回,光所需的时间 2t3 为飞船内的人通过实验计算得到的,另一个处于静态系统的人,观察飞船而测得的时间与此不同。飞船内的人测得的时间就是 2L/c,但是飞船外的测量者测得的时间是:
(2L/c) / SQRT(1-(u/c)2) (Eq#5)
换句话说,当飞船外的观测者望向飞船内的人时,会发现他们点燃雪茄等等动作都变慢了,然而,对于飞船内部的人来说,一切都以正常的节拍进行。因此,不光空间尺度收缩,时间度量设备也会明显慢下来。也就是,如果飞船内的人记录了一个一秒的时间逝去,飞船外的人认为这个时间长度为:
1/SQRT(1 - (u/c)2)
动系中的时钟会变慢确实是一种奇怪的现象,值得研究一番。要理解它,我们需要观察时钟的内部构造,看看在运动的系统中,它里面究竟会发生什么。这很困难,因此我们可以用一个简易的时钟。我们选择的时钟非常简单,但是确实可以按照钟的原理工作:
它是一根杆,两端各是一面镜子,当我们由其一端发射一个光信号,光会在它们之间往返运行,每次到达下方的镜子时就会发出一个“卡塔”的声音信号,就如同一个标准的滴答时钟。
我们制作了两个这样的时钟,相同的长度,并在一开始将它们调为同步;如此,它们就会在之后保持一致,因为它们的长度是一样的,光穿过两端所需的时间是相等的。我们将其中一个让人携带入飞船,并且让钟杆与飞船的运动方向保持垂直关系,这样的时钟的长度就不会收缩。我们如何知道时钟不会收缩呢?在彼此经过的时候,动系和静系中的人可以于各自系统的 y 轴上做好标记。由对称性,两个标记会出现在各自 y 轴的相同的位置,不然的话,当双方一起比较结果的时候,其中一个标记会在另一个标记的上面或者下面,那么我们就可以由此判断谁处在运动的状态。
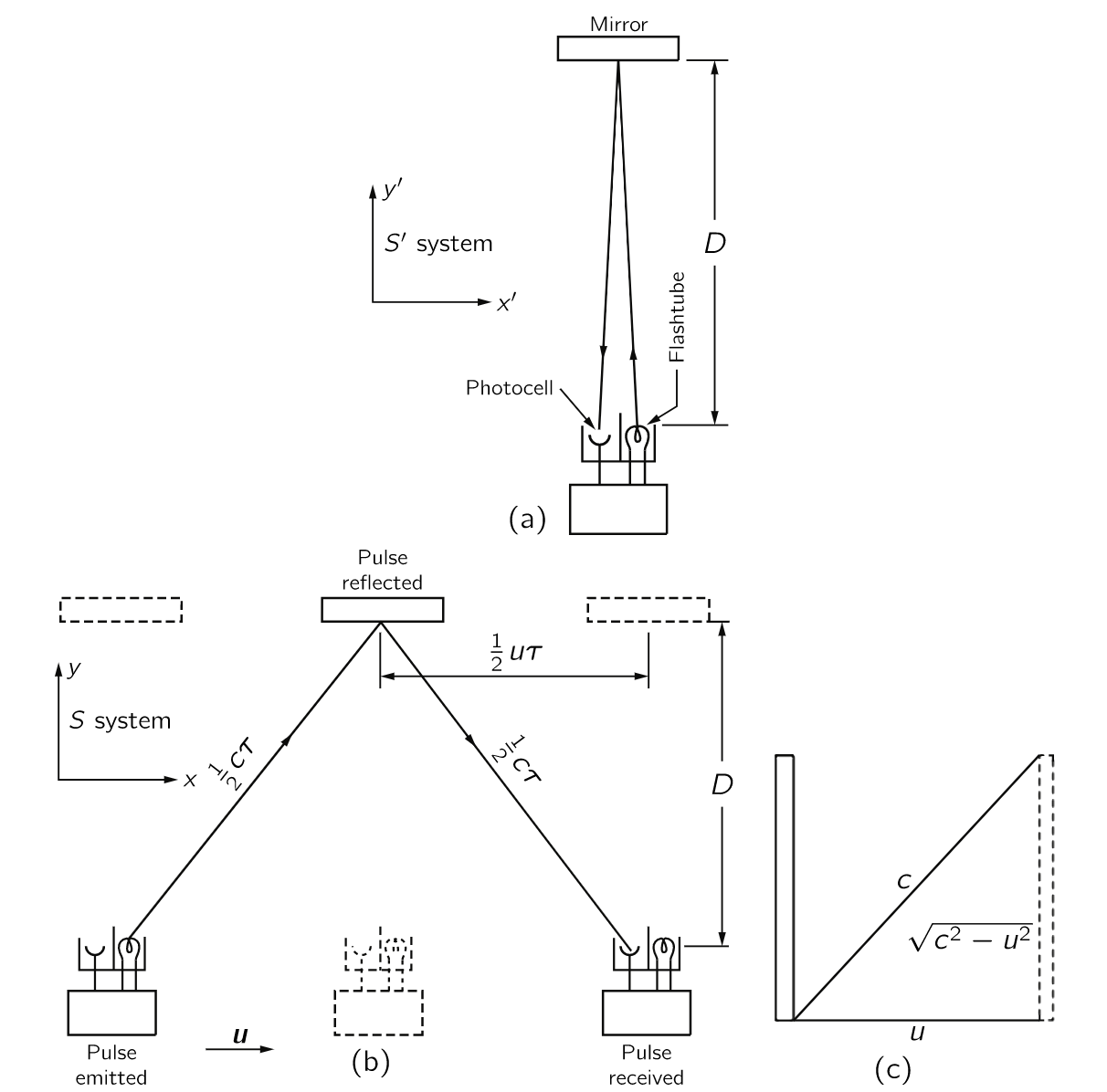
现在,让我们看看运动的时钟内部发生了什么。当 Trump 将它带上飞船之前,Trump 会说它是一个漂亮、标准的时钟,然后 Trump 带着它上了飞船,Trump 还是不能发现什么异常。如果 Trump 发现了什么不同,他就会知道自己在运动 —— 如果有什么事情会因为运动而表现异样,Trump 就能知道他在运动。但是相对性原则告诉我们的是我们不可能在匀速运行的系统中判断出运动与否,因此没什么不一样。另一方面,飞船外的人习近平,在飞船经过他的时候,确实看到了光在时钟的镜面之间的运行轨迹是曲折的,因为钟杆一直都是在运动当中的。我们在 Michelson - Morley 实验那里已经研究过光的这种曲折轨迹。给定一个时间段,杆运行的距离与速度 u 成一定比例,光运行的时间与 c 是成比例的,垂直方向上的距离因此就与 SQRT(c2 - u2) 成比例。
这就是说,对运动的时钟来说,光需要花更多的时间来跑一个来回。因此对于一个运动中的时钟,两次滴答声的时间间隔在表观上更长一些,并且与上面的三角形的弦成比例(这就是方程中出现平方根的原因)。从图可以明显看出,速度 u 越大,时钟就运行得越慢。不光是我们制造的这款时钟的会变慢,如果相对论正确的话,其它的时钟,不管内部运行机制如何,一律都会按照相同的比例慢下来。我们可以不假进一步分析而得知这个结论。这是如何做到的呢?
要回答这个问题,我们需要用到另外两个机械时钟,比如基于齿轮和发条,或者是基于放射性衰变,或者其它机制。我们将这两个时钟与我们的光脉冲时钟调成严格同步。我们的光脉冲时钟每一个来回就会发出一声滴答,新的时钟则在此期间完成了某种循环,它们会即时发出一波闪光,或者发出“嘣”的声音,或者其它信号。其中一个钟被 Trump 带上了飞船,和我们的光脉冲钟一起。也许这个新的时钟并未变慢,它仍然和静止的那个钟以相同的节拍运转,因而和运行的光脉冲时钟存在不一致。啊,这里不对,如果这样的事情是真的,那么 Trump 就会借助这个差异来确定飞船的速度了,而这是不可能办到的。我们不知道这个新的时钟内部发生了什么,导致其变慢了 —— 我们仅仅知道不管原因是什么,它总会慢下来,和我们的光脉冲钟一样。
那么,如果所有的钟都慢下来了,并且没有给出一个测量的办法,仅仅有一个比率,我们只能说,在某种意义上是飞船上的时间本身变慢了。全部的物理现象 —— Trump 的脉搏、思考问题的速度、点燃一根雪茄的时间、长大和变老的时间 —— 全部这些都会以相同的比例慢下来,因为他不能判断他是否处于运动当中。生物学家和医生有时会怀疑说他们不确定癌症的发展过程在运行的飞船上会变缓;但是放在现代物理学家,这几乎是确定的事情,如果不如此,Trump 就可以借此计算飞船的速度了。
跟时间变慢相关,一个有趣的例子是 muon 粒子给出的。Muon 粒子在平均寿命 2.2 x 10-6 秒过后就会自发的分裂。它们会随着宇宙射线到达地球,也可以由实验室人工产生。它们中的有些会在半空中分裂,其它的则会在遇到障碍物之后停止并分裂。很清楚的一点就是,在这么短的时间内,muon 粒子不可能运行 600 米,哪怕它达到光速。但是即便它们在 10 公里远的大气层里产生,我们仍然可以在实验室捕获到一些。这怎么可能呢?答案是不同的 muon 粒子会以不同速度运行,有些接近光速。在它们看来,寿命只有 2 μsec,但是在我们看来,它们的寿命则长到可以观测 —— 长到足够到达地球表面。寿命增长的计算因子就是我们已经知道的:
1 / SQRT(1 - (u / c)2)
对 muon 粒子在不同速度下的平均寿命已经过测量,结果与公式计算出的结果相当接近。
我们不知道为什么 muon 粒子会分裂,内部的机制是什么,但是我们知道它们的表现符合了相对性原则。这就是相对性原则的用处 —— 它可以用来做出预测,甚至是对那些我们尚不了解的事情。举个例子,在我们还不清楚 muon 粒子分裂的原因之前,我们可以预测到当它们以 9 / 10 个光速运行,它们的寿命会延长到:
(2.2×10-6)/ SQRT(1 - (9 / 10)2) sec
我们的预测凑效了 —— 这就是个它给我们带来的好处。
空间变换
现在,让我们看看洛伦兹变换,以尝试对静系和动系之间的关系有一个更好的理解,我们将它们称为 S 和 S’ 系,或者 Joe 和 Moe 的系统。我们已经知道第一个方程式基于洛伦兹的建议;我们如何证明这个收缩效应是真实发生的呢?在 Michelson - Morley 实验中,我们可以肯定的是纵向臂 BC 的长度不会发生改变,这是根据相对性原则而来的;然而,实验的否定结论要求时间必须相等。因此, 为了使实验给出否定结果,横向臂 BE 需要看上去更短,收缩的比例为 SQRT(1 - (u/c)2)。这个收缩是什么意思呢?是 Joe 和 Moe 的测量结果的吗?假设 Moe 随着 S’ 系在 x 方向上移动,他用米尺测量了某点在 x’ 轴上的坐标。他将尺子摆放了 x’ 次,因此他认为这个点离开原点的距离就是 x’ 米。然而在 S 系的 Joe 看来,Moe 使用了一把缩短的尺子,因此真实的距离是 x’ * SQRT(1 - (u/c)2) 米。那么如果 S’ 系远离 S 系一段距离 ut 之后,S 系中的观测者就会说这个相同的点,在他的系统里的位置是 x = x’ * SQRT(1 - (u/c)2),或者:
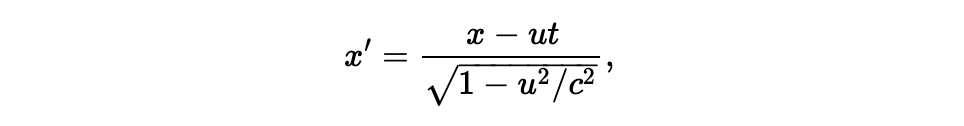
这就是洛伦兹变换方程式。
同时性
采取类似地方式,由时间度量的不同,洛伦兹变换方程式引入了一个分母。在这个方程式中,最有意思的函项是分子中出现的 ux/c2,因为它是那么的新鲜和出乎意料。那么它的物理含义是什么呢?如果我们加以细致考量,会发现,Moe 看到的两个地点同时发生的事件,在 Joe 看来不是同时的。如果一个事件在位置 x1 和时间 t0 发生,另一个事件在 x2 和 t0 (同时的)发生,我们发现这两个时间存在以下差量:
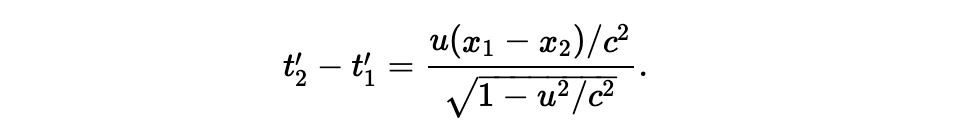
这样的情况被称为“距离引起的同时性失效”,要搞清楚这个事情,我们来考虑如下实验。
假设在飞船里的 Trump (S’ 系统)将两个钟分别放到飞船的两端,他对这个两个钟是否同时很感兴趣。如何将两个钟调成同步呢?有许多方法。说说其中一个,需要我们做一定的计算,首先呢,我们需要一个位置,它位于两个钟的正中间;然后,我们从这个位置向两端发送光信号,光会以相同的速度抵达钟所在的位置,显然,也是同时到达的。如此信号的同时到达可以用于同步时钟。让我们假设 S’ 系统中的 Trump 采用了这种方法。来看看 S 系统中的习近平是否同意飞船中的两个时钟的同步性。Trump 非常确信时钟的同步,因为他不知道自己处在运动之中。但是习近平反对说,由于 Trump 乘坐的飞船在向前跑,在前方的钟会和光信号赛跑,于是光信号不得不跑多于半程的距离才能追上;后方的钟则不然,它与光信号相向运动,因此距离少于半程。所以光信号会先与后方的钟见面,S’ 中的 Trump 还是认为它们同时见面。我们能看到当一个在飞船中的人(比如 Trump)认为两处的时钟是同步的,都为 t’,在其它系统看来它们存在差量。
四维向量
让我们看看能从洛伦兹变换方程式中发现什么。可以注意到针对 x 和 t 的变换形式是很相似的,而对 x 和 y 的做旋转变换的话,我们有:
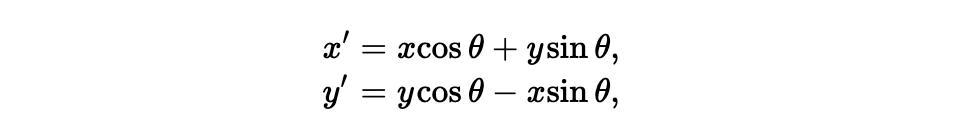
这里,x’ 是对 x 和 y 的混淆计算,y’ 也是如此。类似地,洛伦兹变换中,我们看到 x’ 是对 x 和 t 混淆计算,t’ 是对 t 和 x 混淆。因此洛伦兹变换类似于旋转变换,只是这个旋转是在空间和时间上的,这个观念有点奇特。对如此类比的检验可以通过如下数量计算来进行:
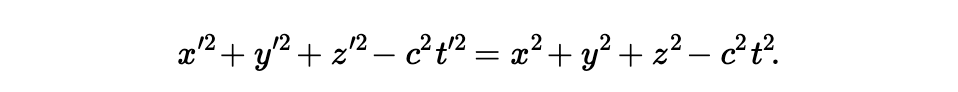
在这个方程式中,两边的前三项表述的含义是在三维空间中,对于当前位置到坐标系原点的距离。某点的距离总是不变的,不考虑轴线的转动。类似地,方程式 Eq#9 表明存在某种混合,它将时间包含进来,对于洛伦兹变换保持不变。由此,将这个变换类比于旋转变换是可取的,它是对于某种向量的变换,同时对于理解相对论也非常管用。
因此,我们对向量的观念有了一些延伸,在此之前我们仅仅考虑到空间分量,现在我们将时间作为一个分量考虑进来。也就是,我们希望有一种四维向量,其中三个表示我们平常理解的空间向量,存在第四个分量与之关联,这就是时间。
我们将在后边几章进一步分析这个概念,那时我们就会发现如果前面提到的这些观念用在动量上,变换就会给出三个空间分量,就如常见的动量向量,和第四个分量 —— 时间 —— 它代表能量。
动力学相对性
我们现在来花点精力研究一下,在洛伦兹变换下,力学定律会呈现出怎样的形式(我们早先了解过长度和时间如何变化,但是没有考虑质量的变化形式 (Eq#1),我们将在下一章做这件事)。要看到爱因斯坦对牛顿力学定律中的 m 项的修正有什么推论,我们从牛顿定律中“力是动量对时间的导数”这点开始:
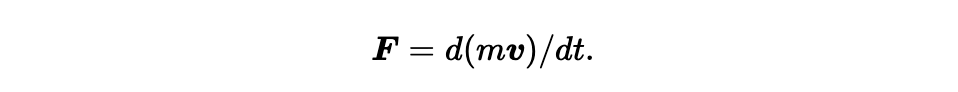
动量还是用 mv 给出,但是我们用新的 m 项时,动量表达为:
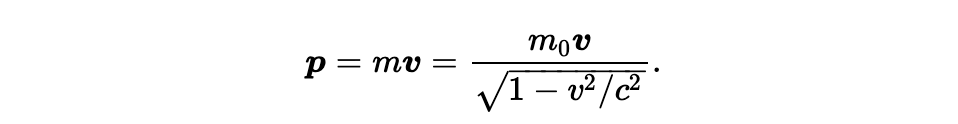
这是爱因斯坦对牛顿定律的修正。如果作用和反作用依然相等的话(可能细节上不对,但是大概如此吧),动量守恒依然和之前一样有效,但是守恒的量不再是基于旧的 mv,而是如上述等式所示,质量存在修正。当加入这项改变之后,动量守恒依然成立。
再来看看动量随速度如何变化。在牛顿的力学里,它是和速度成比例的,根据上式,不管速度如何大小,只要远小于光速,相对论效应就不明显,因为式中的平方根依然非常接近 1;但是如果接近了光速,这个平方根表达式就会趋近零,那么动量就是走向无穷大。
恒定的力作用于一个物体以一段相当久的时间,会发生什么呢?对于牛顿力学,物体会持续不断地提升速度,直到速度超过光速。但是在相对论中这是不可能的。在相对论中,物体依然持续提升,但不是速度,而是动量,动量可以持续增加,因为物体的质量会不断增大。一段时间之后,速度就不再变化了,但动量还在增加。当然,一个力如果对物体的速度的改变起不到多大作用时,我们就说物体的惯性非常大,这就是我们质量相对性公式所要表达的意思 —— 它指出,惯性会随着速度接近光速而变得非常大。举个例子来说明这个效应,为了使电子在 Caltech 里的同步回旋加速器中偏转,我们需要一个比基于牛顿力学的推算强 2000 倍的磁场。换句话说,电子在加速器中的质量是平常的 2000 倍,这跟质子相当。m 2000 倍于 m0 意味着 1 - (u/c)2 必须达到 1 / 4000000,这样 v 只比光速 c 小了 1 / 8000000,电子的速度非常接近光速。如果电子和光都从加速器中出发冲向 Bridge Lab,谁先到达?当然是光了,因为光总是要快一些。要问快多少?这个就很难说了 —— 事实上,我们可以知道光进行的距离超前了多少:大概是 1/1000 英寸,或者是纸张厚度的 1/4!当电子以这般高速运动的时候,它们的质量大得惊人,但是它们的速度依然不能超过光的速度。
现在我们看看基于对质量的相对论修正引起的更多推论。考虑一个装满气体的小容器,里面的分子做着不规则运动。当气体被加温,分子的速度就会增加,因此质量也会增加,气体就会更重。一个近似的计算公式可以表达质量增加的量,在速度很小的情况下,可以利用二项式定理,以幂级数展开:
m0 / SQRT(1- (v/c)2) = m0 (1 - (v/c)2)1/2,
我们就会得到:
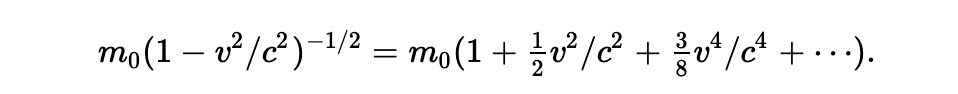
可以清楚的看到,当速度不很大的时候,序列会急剧收敛,第三项之后的诸项可以忽略不计了,因而我们可以这么写:
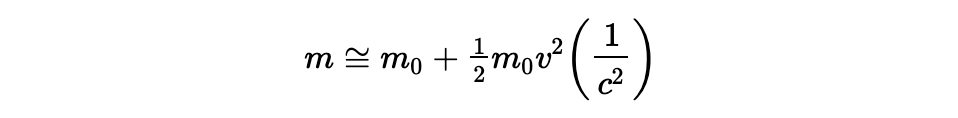
这里,右边的第二项表达的意思是速度的变化如何引起质量的变化。当温度增加,v2 也会线性增加,那么我们就可说质量和温度是成比例关系的。考虑到 1/2 * m0v2 其实是牛顿力学中的动能,我们也可以说容器中气体质量的增加等于动能除以 c 的平方,或者: